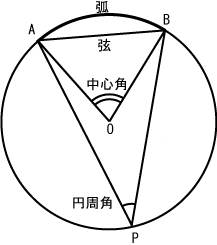
円周角の求め方は意外とシンプルでわかりすいんだ。 円周角の求め方1 「素直に円周角の定理を利用するパターン」 まずは、 円周角の定理を使った求め方 だね。 円周角の定理は、 1つの弧に対する円周角6 = 12 π c m なので、扇形の弧の長さは、 12 π ×Jw_cadにある『 測定 』内の『 角度測定 』の使い方を練習していただくのですが、角度を調べる方法として思いつくのが『 寸法 』タブをクリックした中にある『 角度 』計測機能だと思います。 どちらも指定した角の角度を調べるという点では同じなのですが、測定方法が全く違うものです
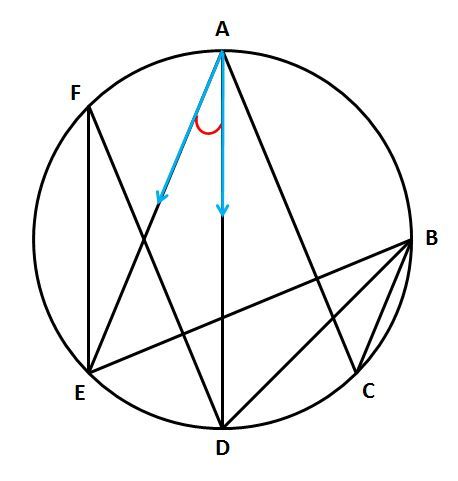
円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
円 角度 求め方
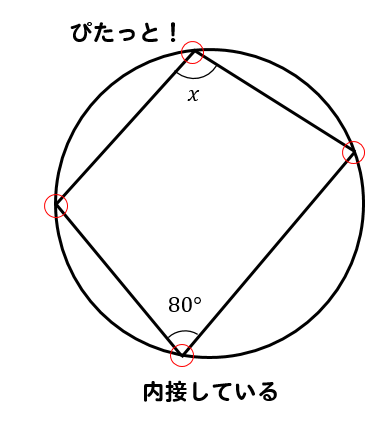
円 角度 求め方-右図において,緑で示した2つの角は,一つの弧 に対する円周角だから等しい. ∠ ABE=60°下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係
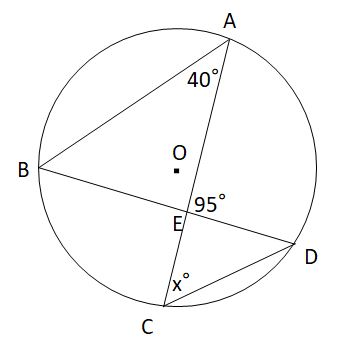
Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer Cancel Confirm Switch camera Shareまた, ∠ AEB は ∠ BEC の補角だから ∠ AEB=180°−110°=70°100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも読める!広告無し!建築学生が学ぶ構造力学のpdf版の学習記事 三角関数の角度は?求め方 三角関数の角度は「三角関数の逆関数」で算定できます。
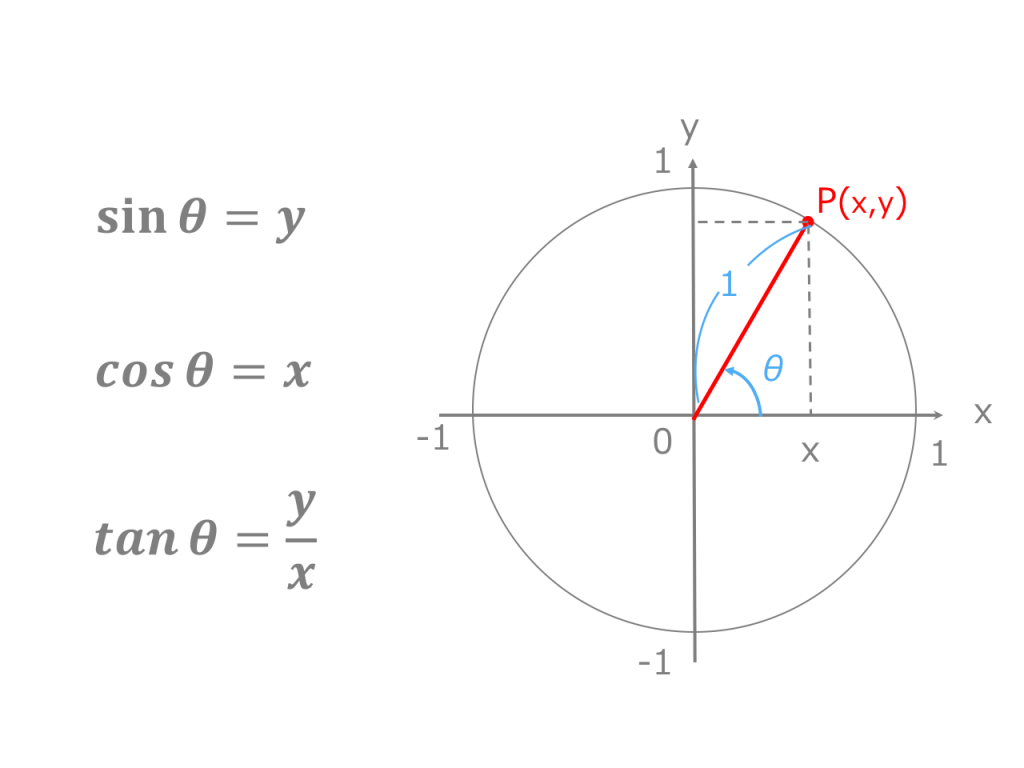
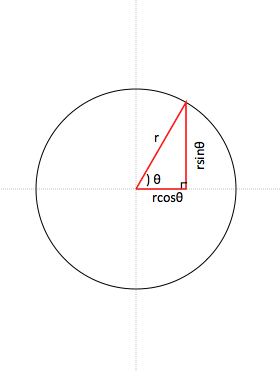
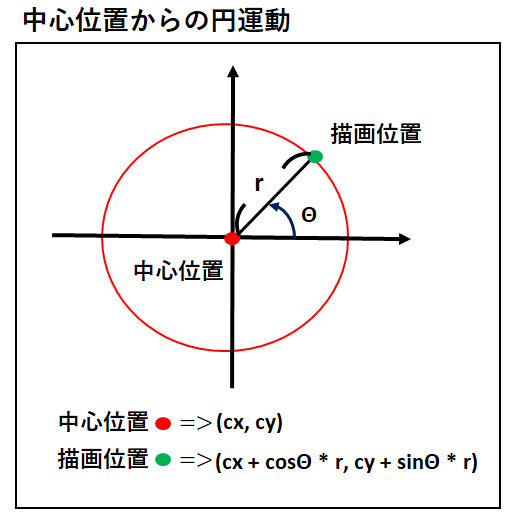
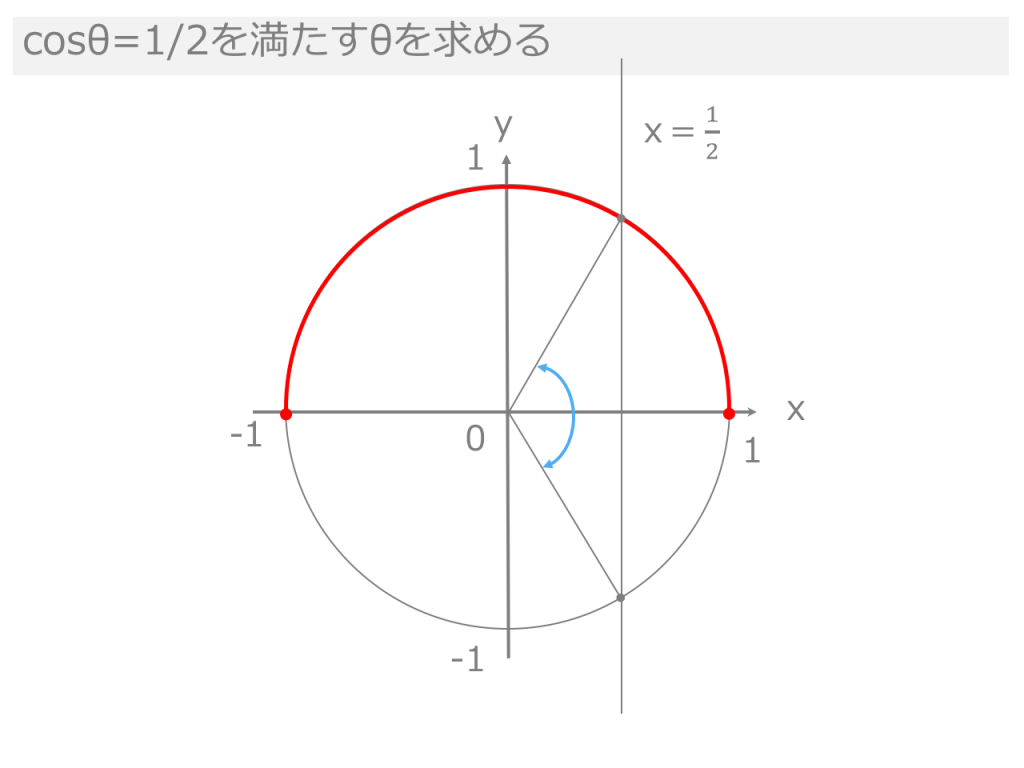
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題結論から言うと、円の中心からx軸に対し、角度θの直線が円周と交わる点の座標 (x, y)は、 (rcosθ, rsinθ)と求められます。 例えば、角度θが45度の場合、座標は (7071, 70,71)、角度θが60度の場合の座標は (5000, 8660)です。三角関数の角度sinを求める①:単位円を利用する \(sinθ=\frac{1}{2}(0<θ<π)\)という方程式の解を求めてみます。 角度を求める上で 単位円(原点中心、半径1の円) を利用します。
その時に必ず必要になるのが単位円の考え方です。 これをマスターするとある角度を言われた時に \(\sin\theta\) はこれぐらい、\(\cos\theta\) はこれぐらいとすぐに言えるようになります。速度・加速度の求め方 │ 受験メモ 図解でわかる円運動を東大院生が解説! 速度・加速度の求め方 高校物理の円運動では、 速度の公式、加速度の公式などなど、 色々と覚える公式が出てきます。 しかし円運動をきっちり理解できている受験生は②正多角形のかき方 ③円周率の求め方(円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を説明し、




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
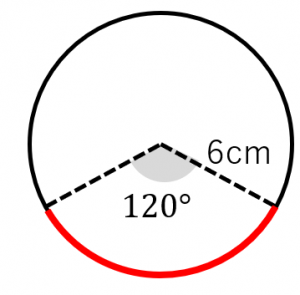
弧の長さ 半径が 6 c m で、中心角が 1 ∘ である扇形の 弧の長さ を計算してみましょう。 円周の長さは 2 π ×弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン法で計算しています。 ※180°以上の中心角の場合、および2つ解がある場合にも対応しました。 動かないA = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学
扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr×となるよ。 ちなみに、この三角形の 2辺は円の半径 でできている、つまり 二等辺三角形X 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 この




円の中心からの角度から真円の円周上の座標を計算する Gamesprit




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
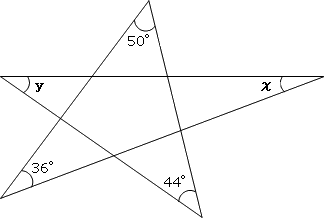
1 360 = 4 π c m となります。 一般に、半径が r で中心角が α ∘ である扇形の弧の長さは、 2 π r ×問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答X 360 l = 2 π r ×




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




扇形の弧の長さの求め方 公式と計算例
α 360 = π r α 180この記事では、三角関数について、角度の求め方や変換公式(\\(90^\\circ − \\theta\\) など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね!『 円の分割方法 』は『 等角度分割 』を応用した使い方ですから、基本的な操作は等角度分割で確認できると思います。 でも、円の分割を行うためには先に少しだけ違う作業が必要になりますので、そのあたりをキャプチャー動画でご覧ください。



円と三角形 角度 中学から数学だいすき



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生
この問題を見て,逆三角関数 tan1 (C言語では atan() や atan2()) を使って CP と CQ の角度をそれぞれ求め, 両者を比較しようと考えた方が多いのではないでしょうか. しかしこの問題では,角度そのものではなく角度差の符号を求めればよいので, 逆三角関数を使う方法よりも簡単で優れた,外積つまり、 軸上で円と重なる点を求めましょう。 ↓の図で言うと点cと点dです。 では実際に、点cと点dの値を求めましょう。 円の中心の座標が(50,0)、円の半径が150なので、三平方の定理こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こ




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
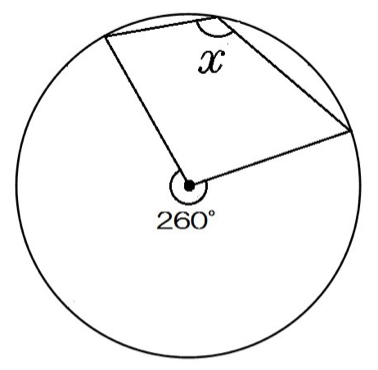
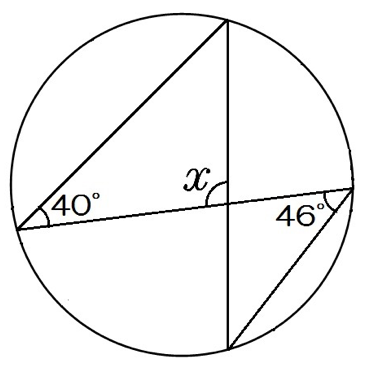
初めに、円の接線 \(at\) と弦 \(ab\) が作る角 \(∠bat<90°\) のとき。 まず、\(ad\) が円の直径になるように、点 \(d\) をとります。 ここで、三角形 \(abd\) に注目すると、以下の4つの式が成り立つことが分かります。40°という角度がヒントになっているけれど、同じ弧に対する円周角や中心角も見当たらないし、使いづらく感じてしまうね。 そこで、 ∠xの方を動かす ことを考えよう。 これは、 同じ弧に対する円周角 が存在するよ。 答えが見えてきたかな? 直径の円周角は、つねに90°半径1の円(「単位円」)の円周上の点$(x, y)$がx軸の正方向と角度$\theta$をなすとき、その座標は$(\cos\theta, \sin\theta)$で表されます。 図001 ️三角関数のsinとcos 高校の数学で、三角関数は直角三角形の辺の比で習ったという方も多いでしょう。それはもう忘れて




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
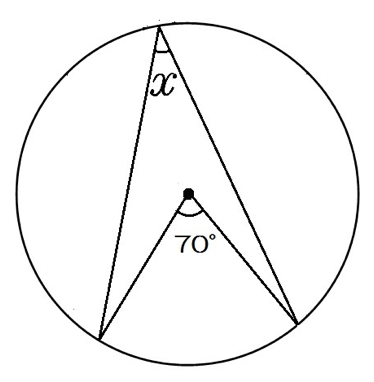
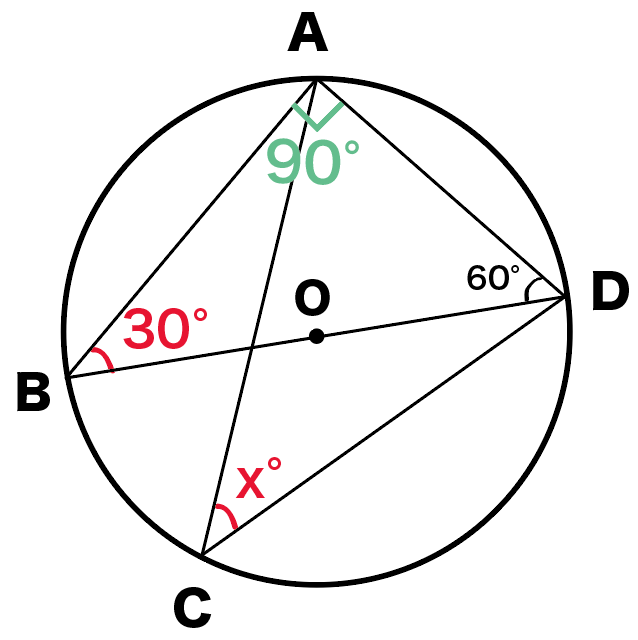
円周角は中心角の半分 同じ弧に対する、 円周角は中心角の半分 だよ。 すると、図の角度が分かるね。 ここから、三角形の 外角の定理 を使うと、 ∠x+50°=100°さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。 中心角はつぎの3ステップで計算できるんだ。 Step1 扇形の中心角をx°とおく まずは「扇形の中心角」を「x°」とおいてみよう。 これは 方程式の文章題 と同じ。 Qikeru:学びを楽しくわかりやすく 5 Pockets 方程式の利用一次方程式の文章題の4つの解き方ア) 外側の大きな円 X 2 Y 2 =a 2 を縦( y )方向に 倍に縮小すると楕円になる. X 2 Y 2 =a 2 , y= Y , x=X → x 2 ( y) 2 =a 2 → =1




本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download
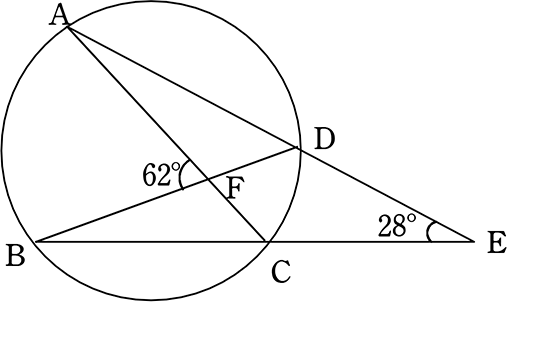



中学数学 円周角 中心角
一般に使われているコピー用紙 (1)上記の図のようにまず紙の中央に折り目を付けてください。 (2)紙の長辺の2つの角が弧の曲線に触れるように配置ください(テープ等で留めてください)。 ※下の写真の 〇 部分 (3)紙の折り目のついた中央部分90deg === 05radian 180deg === 1radian 270deg === 15radian 360deg === 2radian 半径r = 1 を基準にした時の円の 円周 の長さと角度を関連づけている 別の言い方をすると 円周の長さを 2つのr で切り取った長さを rの長さとの比率で表すもの 円周は 直径2r * π なので,ラジアンの基準になる円の円周は 2πとなる 360degの曲率・曲率半径の感覚的な意味と求め方 レベル ★ 最難関大受験対策 極限,微分 更新日時 曲率半径 とは,曲線を「局所的に円の弧」とみなしたときの円の半径。 曲率 とは,曲率半径の逆数。 曲率・曲率半径について解説します。 曲率半径



円周角と中心角の問題について質問があります 画像 のxの角度が30 Yahoo 知恵袋




小5 算数 小5 31 三角形の角 Youtube
円の角度の求め方を教えてください。半径 Yahoo!知恵袋 円の角度の求め方を教えてください。半径343.5cmで円弧の長さが1cmの時、中心角は何度になりますか。よろしくお願いします。 円周率を314とします。また計算の便宜上、1の位は四捨五入しています。円が描けてしまえば、図の幾何学的な関係から以下の式を簡単に導くことができます。 まずは円の半径を下式(5224)で求めます。 ・・・(5228) 主応力、主応力方向までの角度θは以下の式で求めることがでいます。
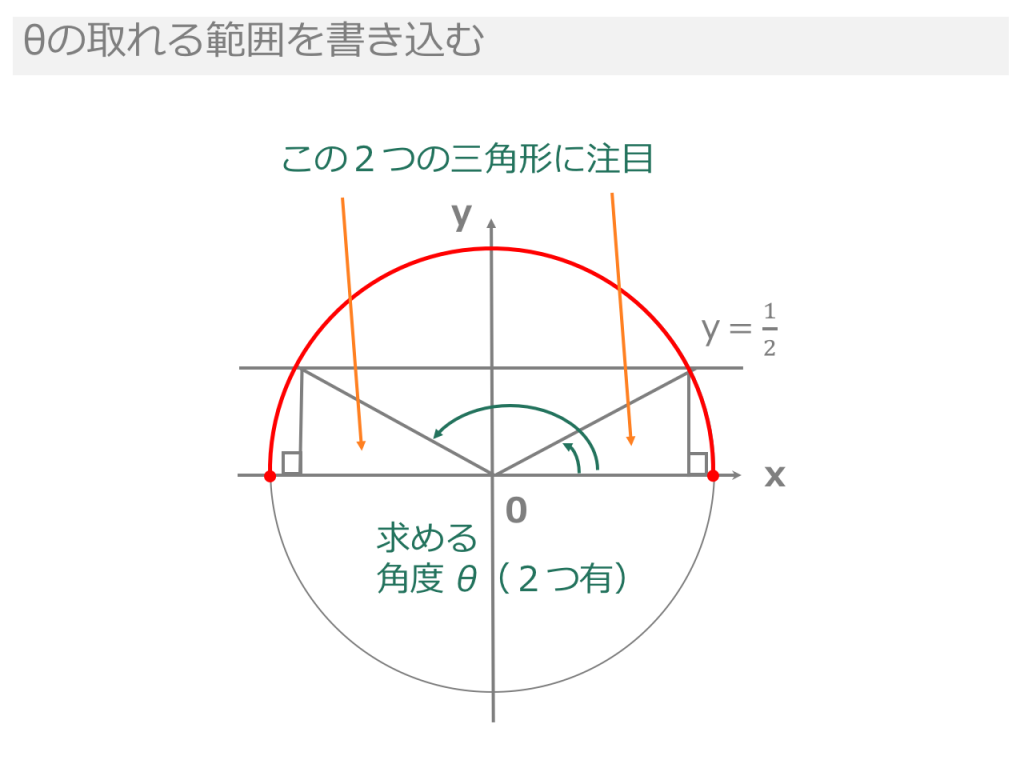



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円周角の定理を使った角度の求め方 写真の問題なんですが適当に書きま Yahoo 知恵袋




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係



1



円と三角形 角度 中学から数学だいすき




Xの角度の求め方を教えて下さい Clear




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円の中にある二つある三角形の角度の求め方 数学 解決済 教えて Goo




接線と円の関係 Jsciencer



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




円周角の定理です Xの角度の求め方を教えてください Clear




円の中の角度を求める高校入試問題を超図解 Youtube




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円に内接する四角形の性質 高校数学の知識庫



角度の求め方 算数の教え上手 学びの場 Com




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



1




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
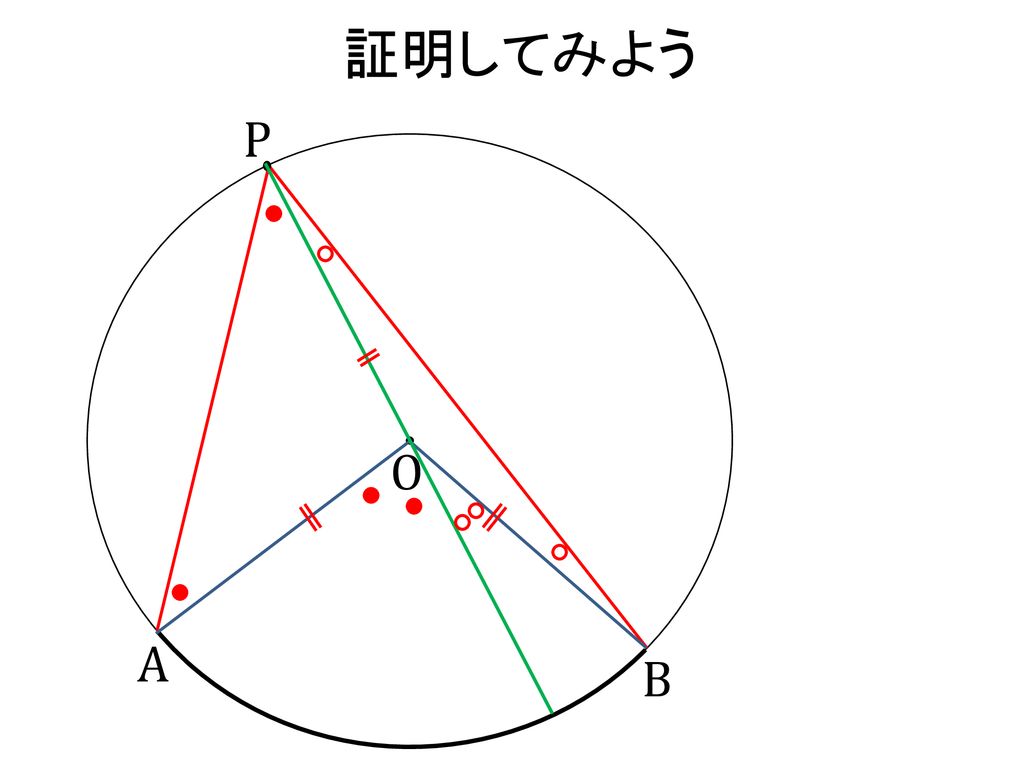



本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
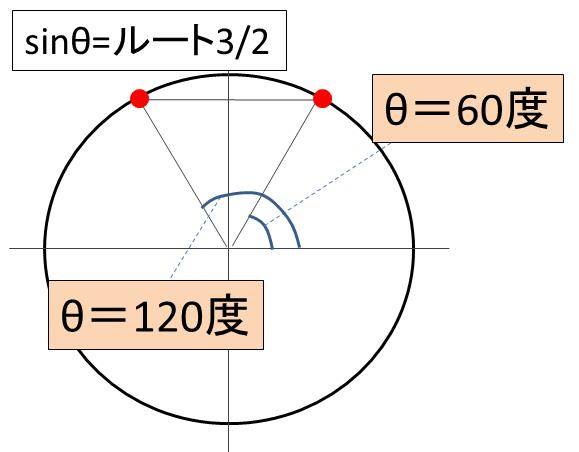



Sin8 1 2の角度 8の値 は Sin8 ルート3 2やsin8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題
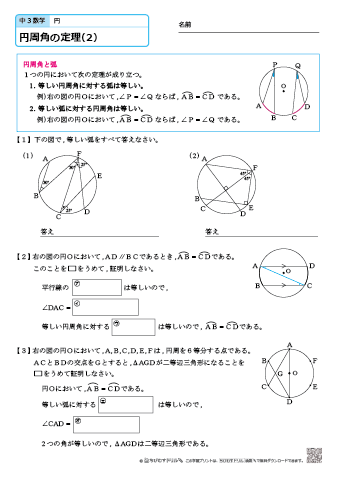



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
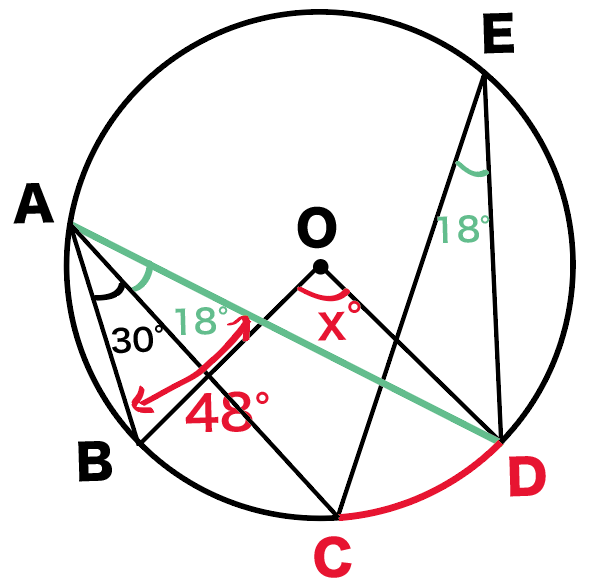



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



円周角の定理と中心角 中学3年数学 Youtube
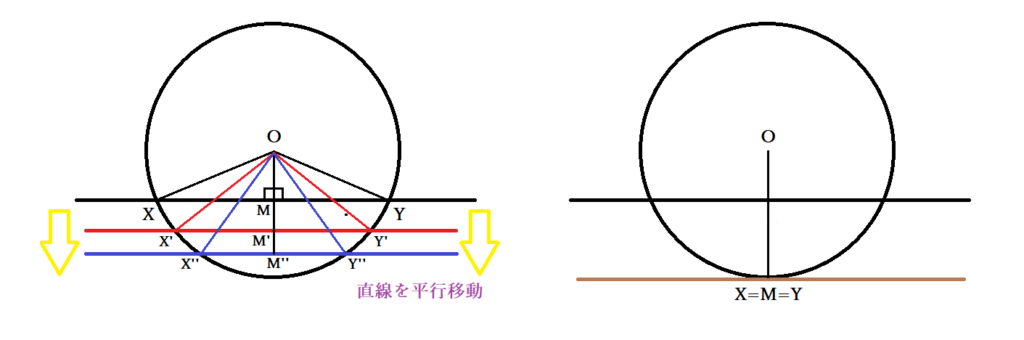



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名



3



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典
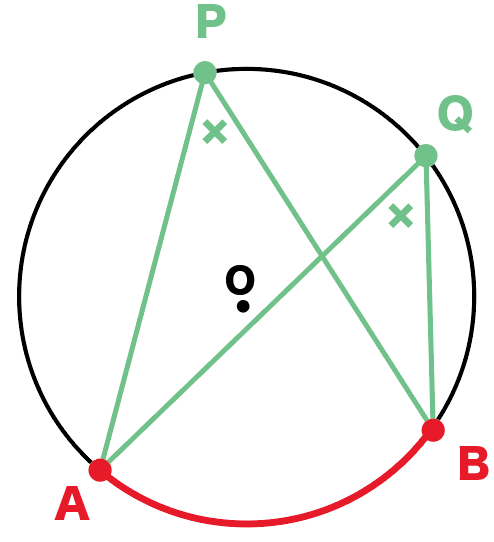



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく
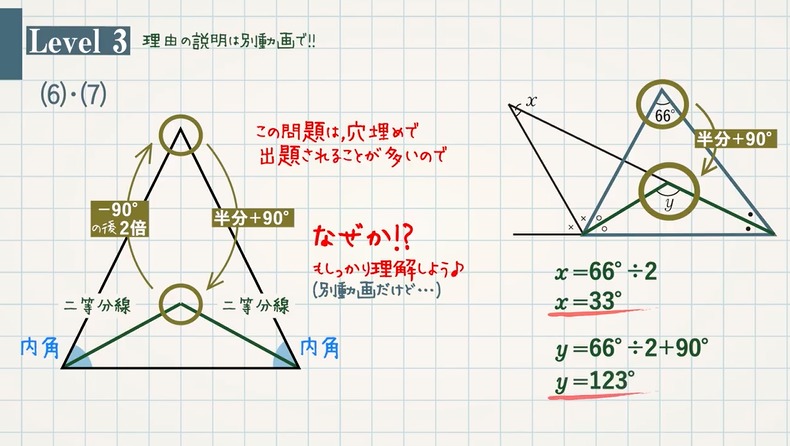



角度の計算 裏技まとめ 教遊者




数学 中3 56 円周角の定理 基本編 Youtube




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
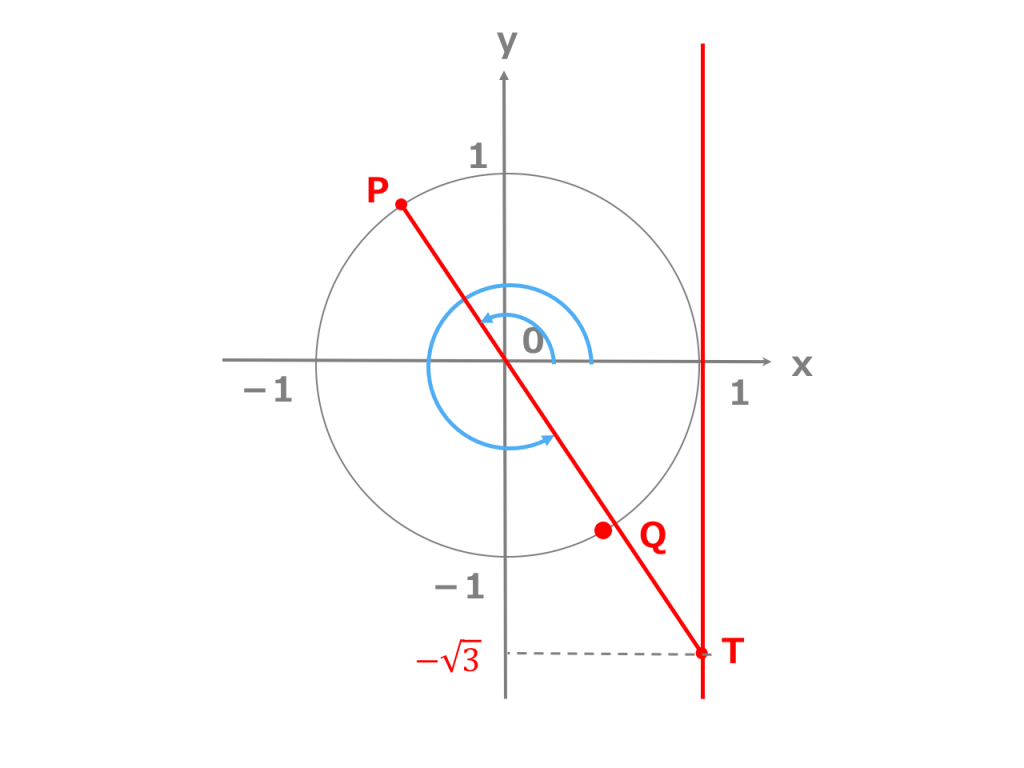



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



円の中心からの角度から真円の円周上の座標を計算する Gamesprit




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



ラングレーの問題 整角四角形




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト




Xの求め方を教えて下さい ちなみに答えは7 8の順で55 71です Clear




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



内接円 内心



プチコン講座 角度計算の基本 ラジアン 三角関数



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
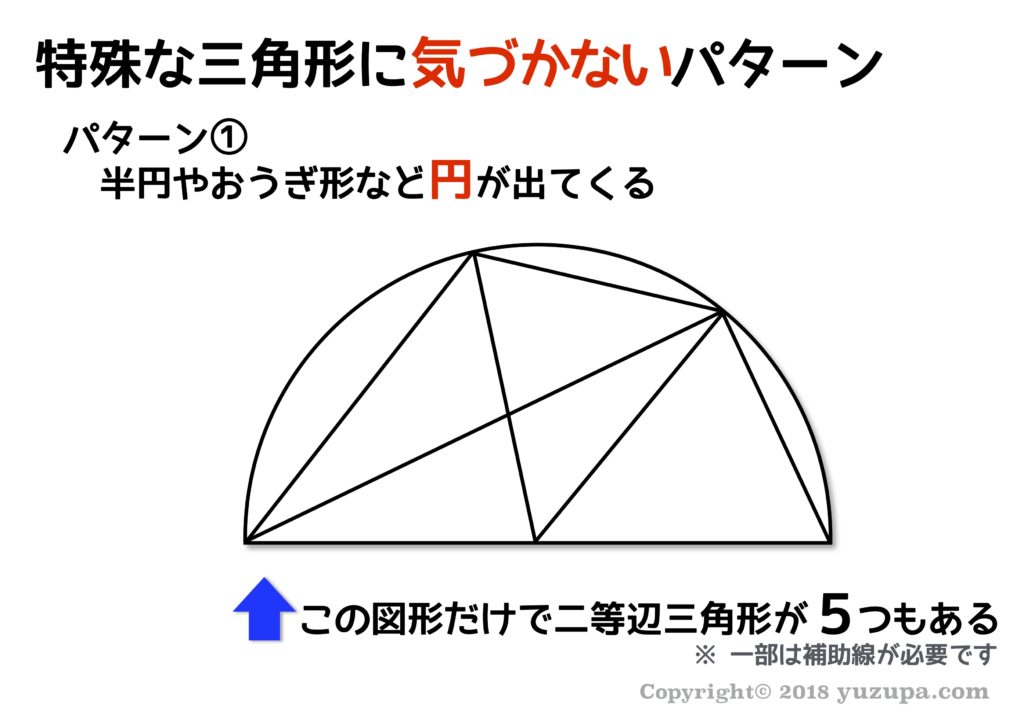



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円周角



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



1



円の中にある三角形の角度の求め方です 上の円の角oac Adcと下の円の角 Yahoo 知恵袋



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




Xの角度の求め方を教えてください 円周角の定理を使う問題です Clear



弧 幾何学 Wikipedia




角度の求め方 算数の教え上手 学びの場 Com




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ



ゲーム 円運動




Circle6 小学校算数 円グラフ Youtube



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



外接円 外心について



10年06月の記事 日曜土木検史郎参上




ラジアン 弧度法 の意味と 度 への変換方法




円周角の定理 角度の計算 中学数学 Youtube




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear



円の接線と角度 中学から数学だいすき



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




ちょうちょ型図形の角度は 求め方を徹底解説 数スタ



タンジェント Tan の求め方を2つ 一歩一歩ぐんぐんブログ
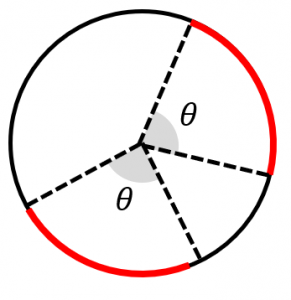



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学



円周角



0 件のコメント:
コメントを投稿